How to Describe the Mean and Standard Deviation in Words

By Vi_Marlie719 18 May, 2022 Post a Comment

Below is the standard deviation formula Standard Deviation Formula Standard deviation SD is a popular statistical tool represented by the Greek letter σ to measure the variation or dispersion of a set of data values relative to its mean. It represents the typical distance between each data point and the mean.

Standard Deviation Problems

The standard deviation SD is a single number that summarizes the variability in a dataset.

. The mean and median are 1029 and 2 respectively for the original data with a standard deviation of 2022. With the help of the variance and standard deviation formula given above we can observe that variance is equal to the square of the standard deviation. Conversely higher values signify that the values spread out further from the mean.

Subtract the mean x from each value. If youre wondering What is the formula for standard deviation it looks like this. Select a single pivotal moment in Elizabeths psychological or moral development in this coming-of-age story taken from Chapters 2838 when Elizabeth is visiting Charlotte Lucas.

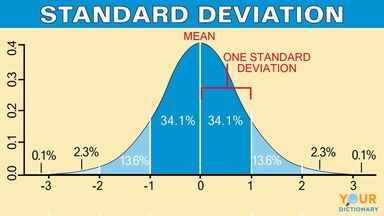
When the elements in a series are more isolated from the mean then the standard. It shows how much variation there is from the average mean. Standard Deviation σ i 1 n x i x 2 n.

For each value x. The fourth column of this table will provide the values you need to calculate the standard deviation. In statistical inference these are commonly known as estimators since they estimate the population parameter values.

μ Expected Value 21. The variance helps determine the datas spread size when compared to the mean value. Xi Data set values.

Where the mean is bigger than the median the distribution is positively skewed. Describe its programs and give one example of an output and an outcome it showcases to describe its impact and effectiveness. Standard deviation SD is a widely used measurement of variability used in statistics.

In the above variance and standard deviation formula. 0 is the smallest value of standard deviation since it cannot be negative. For the logged data the mean and median are 124 and 110 respectively indicating that the logged data have a more symmetrical distribution.

The standard deviation can be affected by outliers in a data set or if the. In order to determine standard deviation. I would say that this suggests that wages are very spread out.

Standard deviation is the square root of the variance calculated by determining the variation between the data points relative to their mean. The median and the mean both measure central tendency. A low standard deviation indicates that the values tend to be close to the mean also called the expected value of the set while a high standard deviation indicates that the values are spread out over a wider range.

Basically a small standard deviation means that the values in a statistical data set are close to the mean or average of the data set and a large standard deviation means that the values in the data set are farther away from the mean. Answer 1 of 9. Standard deviation may be abbreviated SD and is most.

The standard deviation is a measure of how far away your data is from being constant. The standard deviation abbreviated to SD is a measure of variation based on measuring how far each data value deviates from the mean. Standard deviation is the square root of the variance.

The standard deviation of 17 shows how much dispersion there is from the mean wage. Mean to describe the sample with a single value that represents the center of the data. Determine the mean the average of all the numbers by adding up all the data pieces xi and dividing by the number of pieces of data n.

Use the mean to describe the sample with a single value that represents the center of the data. Mean of the data. Square each of those differences.

Many statistical analyses use the mean as a standard measure of the center of the distribution of the data. Precisely the standard deviation is the square root of the variance which is the average of the squared differences from the mean. A low SD indicates that the data points tend to be close to the mean whereas a high SD indicates that the data are spread out over a large range of values.

Add the values in the third column of the table to find the expected value of X. Standard deviation denoted by the symbol σ describes the square root of the mean of the squares of all the values of a series derived from the arithmetic mean which is also called the root-mean-square deviation. A low SD indicates that the data points tend to be close to the mean of the.

The standard deviation measures how concentrated the data are around the mean. Use μ to complete the table. But unusual values called outliers affect the median less than they affect the mean.

A high standard deviation means that values are generally far from the mean while a low standard deviation indicates that values are clustered close to the mean. It might be zero if all the data values are equal. In statistics the standard deviation is a measure of the amount of variation or dispersion of a set of values.

As the variance gets bigger more variation in data. Standard Deviation vs Mean In descriptive and inferential statistics several indices are used to describe a data set corresponding to its central tendency dispersion and skewness. The more concentrated the smaller the standard.

So the standard deviation of 17 is the square root of the average of the squared differences from. -SD can never be negative. The standard deviation is the average amount of variability in your dataset.

It tells you on average how far each value lies from the mean. Smaller values indicate that the data points cluster closer to the meanthe values in the dataset are relatively consistent. A measure of spread that shows how close the values of a set of data are in relation to the mean.

If its zero your data is actually constant and.

Mean And Standard Deviation